螺旋折线

螺旋折线

zhangheng

January 6, 2020

1826 views

No comments

437 words

算法竞赛

题目如下：

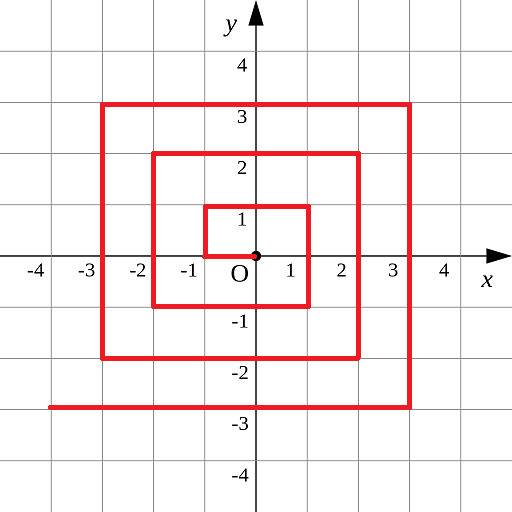
如图所示的螺旋折线经过平面上所有整点恰好一次。

对于整点(X, Y)，我们定义它到原点的距离dis(X, Y)是从原点到(X, Y)的螺旋折线段的长度。

例如dis(0, 1)=3, dis(-2, -1)=9

给出整点坐标(X, Y)，你能计算出dis(X, Y)吗？

【输入格式】

X和Y

对于40%的数据，-1000 <= X, Y <= 1000

对于70%的数据，-100000 <= X， Y <= 100000

对于100%的数据, -1000000000 <= X, Y <= 1000000000

【输出格式】

输出dis(X, Y)

输入
.in
输出
.out
样例输入
0 1
样例输出
3
解题思路：
这里我用的暴力计算，通过观察发现规律，首先我把它分为四个象限每个象限有个中心点满足x=y（第三象限除外，第三象限我定义的是满足x-y=-1）
然后我们就可以围绕这个中心点来计算了，我们通过观察发现：
第一象限的中心点（x，y），到原点的折线距离是：

                         1*2x              例如点（3.3）
                         2*（2x-1）        1*6
                         2*（2x-2）        2*5
                            ...            2*4
                         2*1               2*3    
                                           ...
                                           2*1

第二象限的中心点（x,y）,到原点折线的距离是：

第三象限的中心点（x,y）,到原点折线的距离是（这里注意第三象限的中心点是满足x-y=-1）：

第四象限的中心点（x,y）,到原点折线的距离是：

                         2*2x             
                         2*（2x-1）        
                         2*（2x-2）
                         2*（2x-3）         
                            ...            
                         2*1 

推出这个规律后我们就可以把对应象限的点先用其所在象限的中心点代替计算然后在计算点与中心点的距离
最后就可计算出实际的折现距离了

代码如下：

    
 #include <iostream>


 using namespace std;
 int main()
  {
      int x,y,k;
      int cha,sum=0;
      cin>>x>>y;
      //1象限 
      if(x>=0&&y>=0)//判断象限
       {
           if(x>y)//判断点在中心点的上方还是下方，用于计算实际点与中心点的差值
            {
                cha=x-y;
            y=x;
            }
           else
            {
                cha=x-y;
                x=y;
            }
             sum=2*x;
             k=2*x;
            for(int i=1;i<k;i++)//通过推出的规律累加求得中心点到原点折线距离
             {
                 sum+=2*i;
             }
             sum+=cha;//与求得的差值计算就求出实际点到原点折现的距离
             cout<<sum;
       }
       //2象限
       if(x<0&&y>=0)
        {
            if(y/x<-1)
             {
                 cha=x+y;
                 x=-y;
             }
             else
             {
                 cha=x+y;
                 y=-x;
                 
             }
             k=2*y;
             for(int i=1;i<k;i++)
              {
                  sum+=2*i;
              }
              sum+=cha;
              cout<<sum;
        }
        //3象限 
        if(x<0&&y<0)
         {
             if(x<y)
              {
                  cha=y-x-1;
                  y=x+1;
              }
              else
              {
               cha=y-x-1;
               x=y-1;    
              }
              sum=-2*x-1;
              k=-2*x-1;
              for(int i=1;i<k;i++)
               {
                   sum+=2*i;
               }
               sum+=cha;
               cout<<sum;
         }
         //4象限 
         if(x>=0&&y<0)
          {
              if(y/x>-1)
               {
                   cha=-x-y;
                   y=-x;
               }
               else
               {
                   cha=-x-y;
                   x=-y;
               }
               k=2*x;
               for(int i=1;i<=k;i++)
               {
                   sum+=2*i;
               }
               sum+=cha;
               cout<<sum;
          } 
       
  }

螺旋折线