算法小抄
查找表问题
两个数组的交集 II-350
给你两个整数数组 nums1 和 nums2 ,请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数,应与元素在两个数组中都出现的次数一致(如果出现次数不一致,则考虑取较小值)。可以不考虑输出结果的顺序。
示例 1:
输入:nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2,2]示例 2:
输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出:[4,9]提示:
1 <= nums1.length, nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 1000题解:
分别建立两个map 存储两个数组中每个数的出现次数,以数为key,该数出现的次数为value,
然后对其中一个map进行遍历,如果这个数在两个map都存在那就取出这个数在两个map中出现的最小次数,最后在push相应的次数到结果数组中即可。
function intersect(nums1: number[], nums2: number[]): number[] {
// 交集查询
const map1 = makeCountMap(nums1);
const map2 = makeCountMap(nums2);
const res:number[] = [];
for (const key of map1.keys()) {
const count1 = map1.get(key) as number;
const count2 = map2.get(key);
if(count2) {
const count = Math.min(count1, count2);
for(let i = 0; i < count; i++) {
res.push(key);
}
}
}
return res;
};
function makeCountMap(arr:number[]):Map<number,number> {
const map = new Map();
for (const item of arr) {
if(map.has(item)) {
// 存储每个数出现的次数
map.set(item,map.get(item)+1)
} else {
map.set(item,1)
}
}
return map;
}双指针问题
最接近的三数之和-16
给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数,使它们的和与 target 最接近。
返回这三个数的和。
假定每组输入只存在恰好一个解。
示例 1:
输入:nums = [-1,2,1,-4], target = 1
输出:2
解释:与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。示例 2:
输入:nums = [0,0,0], target = 1
输出:0提示:
3 <= nums.length <= 1000
-1000 <= nums[i] <= 1000
-104 <= target <= 104题解:
首先对数组进行升序排序,然后建立两个指针,left和right left从基准点(从第一个数开始)的下一个数开始,right从最后开始,然后left逐渐向right靠拢,每次移动就将三数的和和目标和的差存储起来,每次都存储最小的差值。如果和大于目标值,说明right的值偏大,就需要将right左移,如果和小于目标值就需要将left右移。
function threeSumClosest(nums: number[], target: number): number {
let min = Infinity;
let res;
if(nums.length === 3) {
return nums[0]+nums[1]+nums[2]
}
// 首先升序排序
nums = nums.sort((a, b) => a - b);
// 取基准点
for(let i = 0; i <= nums.length - 3; i++) {
let base = nums[i];
let left = i+1
let right = nums.length-1;
while(left < right){
let sum = base + nums[left] + nums[right];
let diff = Math.abs(target-sum);
if(diff < min) {
// 记录当前最小值
min = diff;
// 记录最接近的和
res = sum;
}
if(sum < target) {
left++
} else if(sum > target) {
right--;
} else {
return sum;
}
}
}
return res;
};通过删除字母匹配到字典里最长单词-524
给你一个字符串 s 和一个字符串数组 dictionary ,找出并返回 dictionary 中最长的字符串,该字符串可以通过删除 s 中的某些字符得到。
如果答案不止一个,返回长度最长且字母序最小的字符串。如果答案不存在,则返回空字符串。
示例 1:
输入:s = "abpcplea", dictionary = ["ale","apple","monkey","plea"]
输出:"apple"示例 2:
输入:s = "abpcplea", dictionary = ["a","b","c"]
输出:"a"提示:
1 <= s.length <= 1000
1 <= dictionary.length <= 1000
1 <= dictionary[i].length <= 1000
s 和 dictionary[i] 仅由小写英文字母组成题解:
利用双指针,依次遍历每一个单词,如果j指针已经匹配到单词的最后一个就表示这个单词符合条件,再根据字典顺序进行大小比较保存,匹配完之后需要重置两个指针i和j。
var findLongestWord = function(s, dictionary) {
let res = '';
let i = 0;
let j = 0;
for(let item of dictionary){
while(i < s.length && j < item.length){
if(s[i] === item[j]){
i++;
j++;
} else {
i++;
}
if(j === item.length){
res = compare(res, item) < 0 ? item : res;
break;
}
}
i=0;
j=0;
}
function compare(s1,s2) {
if(s1.length > s2.length){
return 1;
} else if(s1.length < s2.length){
return -1
} else {
return s1 < s2 ? 1: -1;
}
}
return res
};搜索二维矩阵 II-240
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
示例 1:
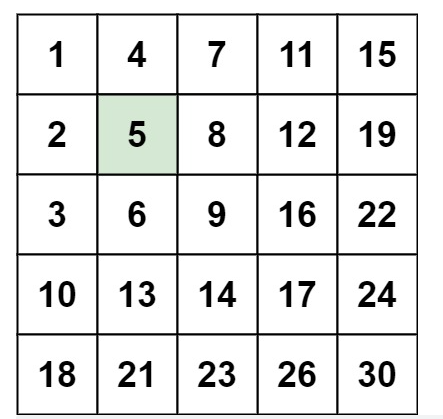
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出:true示例 2:
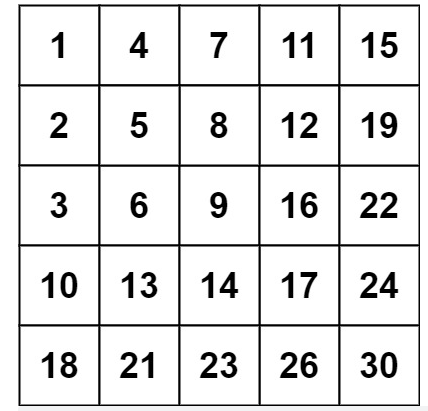
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出:false提示:
m == matrix.length
n == matrix[i].length
1 <= n, m <= 300
-10^9^ <= matrix[i][j] <= 10^9^
每行的所有元素从左到右升序排列
每列的所有元素从上到下升序排列
-10^9^ <= target <= 10^9^题解:
以左下角为例,如果左下角的数小于目标数,那表示所在的一列都是小于目标数的,所以可以使得列数加1,如果左下角的数大于目标数,那表示所在的一行都是大于目标数的,所以可以使得行数减一
var searchMatrix = function(matrix, target) {
const y = matrix.length;
if(y === 0) return false;
x = matrix[0].length;
// 以左下角为参考
let i = 0;
let j = y-1;
while(i < x && j>=0){
const value = matrix[j][i];
if(value === target) return true;
// 左下角的数所在的行都是大于目标数的,可以删去
if(value > target){
j--;
} else {
// 左下角的数所在的一列都是小于目标数
i++;
}
}
console.log(i, j)
return false;
};判断子序列-392
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
进阶:
如果有大量输入的 S,称作 S1, S2, ... , Sk 其中 k >= 10亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
示例 1:
输入:s = "abc", t = "ahbgdc"
输出:true示例 2:
输入:s = "axc", t = "ahbgdc"
输出:false提示:
0 <= s.length <= 100
0 <= t.length <= 10^4
两个字符串都只由小写字符组成。题解:
就是和题目 通过删除字母匹配到字典里最长单词-524一样,只是只匹配一个字符串了
/**
* @param {string} s
* @param {string} t
* @return {boolean}
*/
var isSubsequence = function(s, t) {
let i = 0;
let j = 0;
if(!s.length) return true;
while(i < s.length && j < t.length) {
if(s[i] === t[j]) {
i++;
j++;
} else {
j++;
}
if(i === s.length){
return true;
}
}
return false;
};滑动窗口问题
无重复字符的最长子串-3
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。示例 3:
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。提示:
0 <= s.length <= 5 * 104
s 由英文字母、数字、符号和空格组成题解:
function lengthOfLongestSubstring(s: string): number {
let n = s.length;
let right = -1;
let left = 0;
let max = 0;
let frepWrap = {}// 记录是否有重复的元素
while(left < n) {
let nextWord = s[right+1];
// 没有该元素
if(!frepWrap[nextWord] && nextWord !== undefined) {
frepWrap[nextWord] = 1;
right++;
} else {
//向右移动一位重新开始记录
frepWrap[s[left]] = 0;
left++;
}
max = Math.max(max, right - left +1);
}
return max
};第二种解法:
const lengthOfLongestSubstring = function (s) {
if (s.length === 0) return 0
let max = 0, left = 0;
const map = new Map();
for (let i = 0; i < s.length; i++) {
if (map.has(s[i])) {
// 将重复的第一个元素移动出去,从下一个不重复的开始计数
// 保证获取最大的是因为不要走回头路
left = Math.max(left, map.get(s[i]) + 1);
}
map.set(s[i], i);
// 计算字符串长度,并保留最大值
max = Math.max(max, i - left + 1)
}
return max;
};得到 K 个黑块的最少涂色次数-2379
给你一个长度为 n 下标从 0 开始的字符串 blocks ,blocks[i] 要么是 'W' 要么是 'B' ,表示第 i 块的颜色。字符 'W' 和 'B' 分别表示白色和黑色。
给你一个整数 k ,表示想要 连续 黑色块的数目。
每一次操作中,你可以选择一个白色块将它 涂成 黑色块。
请你返回至少出现 一次 连续 k 个黑色块的 最少 操作次数。
示例 1:
输入:blocks = "WBBWWBBWBW", k = 7
输出:3
解释:
一种得到 7 个连续黑色块的方法是把第 0 ,3 和 4 个块涂成黑色。
得到 blocks = "BBBBBBBWBW" 。
可以证明无法用少于 3 次操作得到 7 个连续的黑块。
所以我们返回 3 。示例 2:
输入:blocks = "WBWBBBW", k = 2
输出:0
解释:
不需要任何操作,因为已经有 2 个连续的黑块。
所以我们返回 0 。提示:
n == blocks.length
1 <= n <= 100
blocks[i] 要么是 'W' ,要么是 'B' 。
1 <= k <= n
通过次数30,783提交次数49,691题解:
方式1 :暴力遍历
/**
* @param {string} blocks
* @param {number} k
* @return {number}
*/
var minimumRecolors = function(blocks, k) {
let min = Infinity;
for(let i=0; i<=blocks.length-k;){
for(let j=k;j<=blocks.length;){
const bNums = blocks.slice(i,j).split('').filter(item => item === 'B').length;
console.log(bNums)
min = Math.min(min, k-bNums)
i++;
j++;
}
}
return min
};方式2:滑动窗口
首先遍历第一个长度为k的窗口,确定需要操作的个数(白色的个数),接下来按照这个区间开始滑动,当右边遇到一个白色的就将操作数加1,当左边滑出一个白色的就将操作数减1,每次滑动的同时比较保留操作数最小的。
/**
* @param {string} blocks
* @param {number} k
* @return {number}
*/
var minimumRecolors = function(blocks, k) {
let cnt = 0;
let l = 0; let r = 0;
// 算出第一个窗口的操作数
while(r<k){
if(blocks[r] === 'W'){
cnt++;
}
r++;
}
// 这里要重新赋值一个副本,用于比较
let res = cnt;
while(r < blocks.length){
// 注意索引
if(blocks[r] === 'W') res++;
if(blocks[l] === 'W') res--;
cnt = Math.min(cnt, res);
l++;
r++;
}
return cnt
};链表问题
两两交换链表中的节点-24
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
示例 1: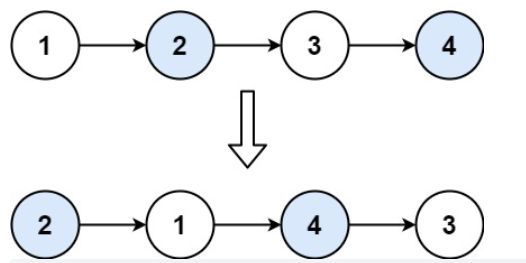
输入:head = [1,2,3,4]
输出:[2,1,4,3]示例 2:
输入:head = []
输出:[]示例 3:
输入:head = [1]
输出:[1]提示:
链表中节点的数目在范围 [0, 100] 内
0 <= Node.val <= 100题解:
- 找终止条件:本题终止条件很明显,当递归到链表为空或者链表只剩一个元素的时候,没得交换了,自然就终止了。
- 找返回值:返回给上一层递归的值应该是已经交换完成后的子链表。
- 单次的过程:因为递归是重复做一样的事情,所以从宏观上考虑,只用考虑某一步是怎么完成的。我们假设待交换的俩节点分别为head和next,next的应该接受上一级返回的子链表(参考第2步)。就相当于是一个含三个节点的链表交换前两个节点,就很简单了,想不明白的画画图就ok。
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @return {ListNode}
*/
var swapPairs = function(head) {
if(head === null || head.next === null) return head;
let next = head.next;
head.next = swapPairs(next.next);
next.next = head;
return next;
};反转链表-206
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
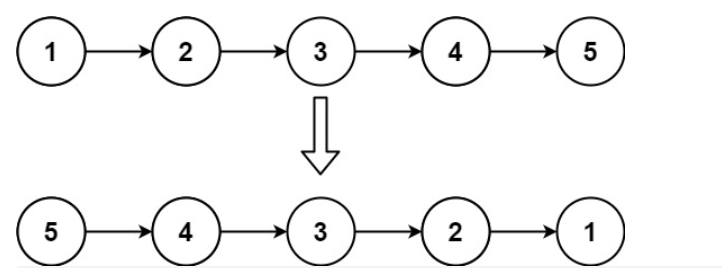
示例一:
输入:head = [1,2,3,4,5]
输出:[5,4,3,2,1]题解:
非递归法和递归法,将第一个节点和第二个节点进行交换,递归法就是将剩下的节点看作一个整体和第一个进行交换,终止条件就是当遇到最后一个节点或者链表为空
非递归法:
/**
* Definition for singly-linked list.
* class ListNode {
* val: number
* next: ListNode | null
* constructor(val?: number, next?: ListNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
* }
*/
// 非递归法
function reverseList(head: ListNode | null): ListNode | null {
let prev = null;
let cur = head;
while(cur) {
const oldCurNext = cur.next;
cur.next = prev;
// 更新节点
prev = cur;
cur = oldCurNext;
}
return prev;
};递归法:
/**
* Definition for singly-linked list.
* class ListNode {
* val: number
* next: ListNode | null
* constructor(val?: number, next?: ListNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
* }
*/
function reverseList(head: ListNode | null): ListNode | null {
if (head === null || head.next === null) return head;
const newHead = reverseList(head.next);
head.next.next = head;
head.next = null;
return newHead;
};
深度优先遍历
二叉树的所有路径-257
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。叶子节点 是指没有子节点的节点。
示例 1:
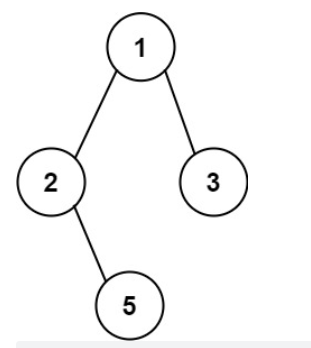
输入:root = [1,2,3,null,5]
输出:["1->2->5","1->3"]示例 2:
输入:root = [1]
输出:["1"]题解:
深度优点的体现,用当前节点的值去拼接左右子树递归调用当前函数获得的所有路径。也就是根节点拼上以左子树为根节点得到的路径,加上根节点拼上以右子树为根节点得到的所有路径。直到叶子节点,仅仅返回包含当前节点的值的数组。
let binaryTreePaths = function (root) {
let res = []
if (!root) {
return res
}
if (!root.left && !root.right) {
return [`${root.val}`]
}
let leftPaths = binaryTreePaths(root.left)
let rightPaths = binaryTreePaths(root.right)
leftPaths.forEach((leftPath) => {
res.push(`${root.val}->${leftPath}`)
})
rightPaths.forEach((rightPath) => {
res.push(`${root.val}->${rightPath}`)
})
return res
}递归与回溯
电话号码的字母组合-17
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

示例 1:
输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]示例 2:
输入:digits = ""
输出:[]示例 3:
输入:digits = "2"
输出:["a","b","c"]提示:
0 <= digits.length <= 4
digits[i] 是范围 ['2', '9'] 的一个数字。题解:此题也是类似于商品的SKU组合,从每一组里取出一个数进行组合,所以我们首先列出所有的数字对应的数组。根据输入的数字过滤出对应分分组。从第一个分组开始遍历单个分组中的数据,取出第一个分组的一个数据后再递归处理后续分组中的数据,终止条件是取出的数据长度等于分组的长度,即每个分组的数据都取到了这样就完成了一次组合。
var letterCombinations = function(digits) {
if(!digits) return [];
const res = [];
const numberMap = {
2:'abc',
3:'def',
4:'ghi',
5:'jkl',
6:'mno',
7:'pqrs',
8:'tuv',
9:'wxyz'
}
const groups = digits.split('').map(item => numberMap[item]);
function helper(index, prev){
if(groups.length === index){
return res.push(prev.join(''))
}
const chunk = groups[index];
for (const item of chunk) {
let cur = prev.concat(item);
helper(index+1, cur);
}
}
helper(0, []);
return res;
};相关拓展:商品SKU组合
字母大小写全排列-784
给定一个字符串 s ,通过将字符串 s 中的每个字母转变大小写,我们可以获得一个新的字符串。
返回 所有可能得到的字符串集合 。以 任意顺序 返回输出。
示例 1:
输入:s = "a1b2"
输出:["a1b2", "a1B2", "A1b2", "A1B2"]示例 2:
输入: s = "3z4"
输出: ["3z4","3Z4"]提示:
1 <= s.length <= 12
s 由小写英文字母、大写英文字母和数字组成题解: 这个题和一些组合类相关的代码类似,首先将字符串一个一个的遍历并且处理拼接,当遇到数字就原封不动的拼接并进入下一递归,如果遇到字母就转换为大写和小写进行在分别递归。当拼接的长度刚好等于原字符串的长度时就保存退出。
/**
* @param {string} s
* @return {string[]}
*/
var letterCasePermutation = function (s) {
if (!s) return;
const res = [];
function helper(prev, nextStr) {
if (prev.length === s.length) {
res.push(prev);
return;
}
let item = nextStr[0];
nextStr = nextStr.slice(1);
if (/\d/.test(item)) {
let cur = prev + item;
helper(cur, nextStr);
} else if (/[a-zA-Z]/.test(item)) {
let cur1 = prev + item.toUpperCase();
let cur2 = prev + item.toLowerCase();
helper(cur1, nextStr);
helper(cur2, nextStr);
}
}
helper("", s);
return res;
};面试题 08.08. 有重复字符串的排列组合
有重复字符串的排列组合。编写一种方法,计算某字符串的所有排列组合。
示例1:
输入:S = "qqe"
输出:["eqq","qeq","qqe"]示例2:
输入:S = "ab"
输出:["ab", "ba"]提示:
字符都是英文字母。
字符串长度在[1, 9]之间。题解:
每轮递归中循环当前剩余的单词,尝试以单词中的每个字母拼接在上次递归后形成的字符串后面,并且用剩下的字母继续递归拼接,直到拼接的长度等于 S 的长度,即可作为一个结果放入 res 中。
注意剪枝部分的逻辑,每轮递归中,假设我们已经尝试过用 q 来拼接了,那么就记录在这轮递归的 visited 中,循环中再遇到 q 直接跳过即可,因为得到的结果一定是重复的。
/**
* @param {string} S
* @return {string[]}
*/
var permutation = function(s) {
const size = s.length;
const res = []
function helper(prev, rest){
if(prev.length === size){
res.push(prev);
return;
}
let cache = {}
for (let i=0;i<rest.length;i++) {
if( cache[rest[i]]) continue;
cache[rest[i]] =true;
helper(prev+rest[i], rest.slice(0,i)+rest.slice(i+1))
}
}
helper('',s)
return res;
};子集 II-90
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
示例 1:
输入:nums = [1,2,2]
输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]示例 2:
输入:nums = [0]
输出:[[],[0]]提示:
1 <= nums.length <= 10
-10 <= nums[i] <= 10题解
此题相较于子集就是加了个去重,首先我们需要对数组进行排序,这样生成重复的组合就会挨在一起,所以我们只需要判断前面一个递归是不是和本次递归的起始元素是否相等就可以了。相等就不处理,这样就避免重复的起始元素进入递归生成重复的组合了。
/**
* @param {number[]} nums
* @return {number[][]}
*/
var subsetsWithDup = function(nums) {
let ret = []
nums = nums.sort((a, b) => a-b)
let helper = (start, prev) => {
ret.push(prev)
for (let i = start; i < nums.length; i++) {
// 去重逻辑
if (i > start && nums[i] == nums[i - 1] ) {
continue;
}
helper(i+1, prev.concat(nums[i]))
}
}
helper(0, [])
return ret
};组合总和-39
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]示例 3:
输入: candidates = [2], target = 1
输出: []提示:
1 <= candidates.length <= 302 <= candidates[i] <= 40candidates的所有元素 互不相同1 <= target <= 40
思路:
这道题就是将 子集II 的去重逻辑去掉。之前的递归,我们对于 helper 递归函数每次递归都会把 start 起点 +1,如果我们每次递归不去 +1,而是把 start也考虑在内的话,就可以把重复元素的情况也考虑进去了
/**
* @param {number[]} candidates
* @param {number} target
* @return {number[][]}
*/
var combinationSum = function(candidates, target) {
const res = [];
function helper(start, prev, sums){
if(prev === target){
res.push(sums);
return
}
for(let i=start;i<candidates.length;i++){
if(prev < target){
const cur = sums.concat(candidates[i]);
helper(i,prev+candidates[i],cur);
} else {
continue;
}
}
}
helper(0,0, []);
return res;
};组合总和 II-40
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]提示:
1 <= candidates.length <= 100
1 <= candidates[i] <= 50
1 <= target <= 30题解
相比较 组合总和,这道题就是加了个去重逻辑,而去重逻辑也可以借助 子集II 的思路
/**
* @param {number[]} candidates
* @param {number} target
* @return {number[][]}
*/
var combinationSum2 = function(candidates, target) {
const res = [];
if(!candidates.length) return res;
candidates.sort((a, b) => a-b)
function helper(start,prev, curArr){
if(prev === target){
res.push(curArr);
return;
}
for(let i = start; i< candidates.length;i++){
if(prev < target) {
if(i>start&&candidates[i]==candidates[i-1])
{
continue;
}
const cur = curArr.concat(candidates[i]);
helper(i+1, prev+candidates[i], cur);
} else {
continue;
}
}
}
helper(0, 0, []);
return res;
};组合总和 III-216
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
只使用数字1到9
每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。示例 3:
输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字,我们可以得到的最小和是1+2+3+4 = 10,因为10 > 1,没有有效的组合。提示:
2 <= k <= 9
1 <= n <= 60题解
思路和 组合总和II 一样 ,总之 组合总和1-3 都可以根据 子集II 的思路进行解答
/**
* @param {number[]} candidates
* @param {number} target
* @return {number[][]}
*/
var combinationSum3 = function(k,n) {
const res = [];
const candidates = generateArray(9);
// 创建一个map,记录每个数的个数
function helper(start,prev, curArr){
if(curArr.length === k && prev === n){
res.push(curArr);
return;
}
for(let i = start; i< candidates.length;i++){
if(prev < n) {
if(i>start&&candidates[i]==candidates[i-1])
{
continue;
}
const cur = curArr.concat(candidates[i]);
helper(i+1, prev+candidates[i], cur);
} else {
continue;
}
}
}
helper(0, 0, []);
return res;
function generateArray(n) {
const result = [];
for (let i = 1; i <= n; i++) {
result.push(i);
}
return result;
}
};全排列 II-46
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]提示:
1 <= nums.length <= 8
-10 <= nums[i] <= 10题解:
相比较 全排列 这次是给的有重复数字的数组,并且要求返回不重复的全排列 所以整体思路是一直的,我们只需要考虑如何去重即可。去重方式是首先将数组排序,这样就能保证相同的元素紧挨在一起,这样我们第一次回溯后,第二次的递归在开始我们就判断当前的元素是否和上一次的元素相等,如果相等就跳过此次递归,这样就能保证同样的结果再次输出
var permuteUnique = function(nums) {
const res = [];
if(!nums.length) return;
nums.sort()
const visted = {};
function helper(cur, temp){
if(cur.length === nums.length){
res.push(cur);
return;
}
for(let i = 0; i < temp.length; i++){
// 去重关键
if(visted[temp[i]] < i && temp[i] === temp[i-1]){
continue;
}
visted[temp[i]]= i;
let arr = cur.concat(temp[i]);
const nextArr = [...temp.slice(0,i), ...temp.slice(i+1)];
helper(arr, nextArr);
}
}
helper([], [...nums]);
return res;
};还有一种方式就是使用一个对象存储已经组合好的排列的数组字符串,相比较上面的方法该方法比较耗费空间,但是很好理解
var permuteUnique = function(nums) {
const res = [];
if(!nums.length) return;
const used = {};
function helper(cur, temp){
if(cur.length === nums.length){
// 判断是否已经有该组合了
if(!used[cur.toString()]) {
res.push(cur);
}
used[cur.toString()] = true;
return;
}
for(let i = 0; i < temp.length; i++){
let arr = cur.concat(temp[i]);
const nextArr = [...temp.slice(0,i), ...temp.slice(i+1)]
helper(arr, nextArr);
}
}
helper([], [...nums]);
return res;
};全排列-46
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]示例 3:
输入:nums = [1]
输出:[[1]]提示:
1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数 互不相同题解:
首先是不含重复数字的数字,我们可以直接套用递归回溯的公式进行解答
function permute(nums: number[]): number[][] {
const res = [];
if(!nums.length) return;
function helper(cur, temp){
if(cur.length === nums.length){
// 判断是否已经有该组合了
res.push(cur);
return;
}
for(let i = 0; i < temp.length; i++){
let arr = cur.concat(temp[i]);
const nextArr = [...temp.slice(0,i), ...temp.slice(i+1)]
helper(arr, nextArr);
}
}
helper([], [...nums]);
return res;
};当然dfs也可以
function permute(nums: number[]): number[][] {
const res = [];
const temp = [];// 保存当前正在访问的数组
function dfs(){
if(nums.length === temp.length){
res.push([...temp])
return;
}
nums.forEach((val) => {
if(!temp.includes(val)) {
temp.push(val);
dfs();
temp.pop();
}
})
}
dfs()
return res
};分割回文串-131
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
示例 1:
输入:s = "aab"
输出:[["a","a","b"],["aa","b"]]示例 2:
输入:s = "a"
输出:[["a"]]提示:
1 <= s.length <= 16
s 仅由小写英文字母组成题解:
首先我们需要写出一个判断当前字符串是否为回文的函数,然后在套用递归回溯的模板,将递归条件设置为是回文字符串就继续递归判断剩余的字符串,返回条件就是当判断到字符串最后一位的时候就返回。最后注意一次递归结束后需要删除当前递归开始放入的元素再向字符串右边扩散继续判断回文。
var partition = function (s) {
const res = [];
const temp = [];
function helper(start) {
if(start >= s.length) {
res.push([...temp])
return;
}
for(let i = start; i < s.length;i++) {
if(isPalindrome(start, i)){
temp.push(s.slice(start, i+1))
helper(i+1);
} else {
continue;
}
// 这个区间的字符串已经递归完了,删除后再右移判断
temp.pop();
}
}
helper(0)
// 判断字符串是否为回文子串
function isPalindrome(m, n) {
//判断是否越界
while (m<n) {
if( s[m] !== s[n]){
return false;
}
m++;
n--;
}
return true;
}
return res;
};复原 IP 地址-93
有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。
例如:"0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址,但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效 IP 地址。
给定一个只包含数字的字符串 s ,用以表示一个 IP 地址,返回所有可能的有效 IP 地址,这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。
示例 1:
输入:s = "25525511135"
输出:["255.255.11.135","255.255.111.35"]示例 2:
输入:s = "0000"
输出:["0.0.0.0"]示例 3:
输入:s = "101023"
输出:["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]提示:
1 <= s.length <= 20
s 仅由数字组成题解:
此题也是和分割回文字符串思路一样,只是把递归返回的条件改一下,改成是否是一个有效的ip地址即可
var restoreIpAddresses = function(s) {
const res = [];
if(!s.length) return res;
const temp = [];
function helper(start) {
if(temp.length === 4 && start >= s.length){
res.push([...temp]);
return;
}
for(let i = start; i< start+3;i++) {
if(checkIp(s.slice(start,i+1))){
temp.push(s.slice(start,i+1));
helper(i+1);
} else {
continue;
}
temp.pop()
}
}
helper(0)
// 是否是一个有效的ip地址
function checkIp(s) {
if(s.length === 0) return false;
if(s[0] === '0' && s.length !== 1) return false;
if(+s >= 0 && +s <=255) return true;
return false;
}
return [...new Set(res.map(item => item.join('.')))];
};括号生成-22
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例 1:
输入:n = 3
输出:["((()))","(()())","(())()","()(())","()()()"]示例 2:
输入:n = 1
输出:["()"]提示:
1 <= n <= 8题解:
利用回溯法,不断的朝着前一个结果的尾部追加左括号或者右括号,即可枚举出全部结果。
注意条件限制,由于我们是只往尾部添加括号,所以右括号的使用数量不能大于左括号,否则无法形成结果,比如())这种就不可能在往尾部追加其他括号的情况下得到一个解。
利用变量 left、right 分别记录剩余的左右括号数量,利用 prev 记录上一轮递归中已经形成的中间结果,当 left 和 right 都为 0,就得到一个结果,记录进 res 中。
/**
* @param {number} n
* @return {string[]}
*/
var generateParenthesis = function(n) {
const res = [];
function helper(left, right, cur) {
if(left < 0 || right < 0 || right < left) {
return;
}
if(left === 0 && right === 0) {
res.push(cur);
return
}
helper(left-1, right, cur+'(');
helper(left, right-1, cur+')')
}
helper(n,n,'')
return res;
};
查找
二分查找-704
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1提示:
你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。题解:
经典的查找算法。对于升序排列的数组,我们首先以数组索引中间值将数组分为两部分,将目标数和中间数进行比较,如果大于的话就在较大的那一部分里继续分组这个操作,否则就在较小的那一部分里进行分组。找到找完或者找到目标数。
注意注意一些细节,为什么left是小与等于right而不是小于right,为什么分组后要将mid加一再赋值给left或者right。
var search = function(nums, target) {
let left = 0;
let right = nums.length - 1;
while(left <= right){
const mid = Math.floor((left + right) / 2);
if(target > nums[mid]){
left = mid+1;
} else if(target < nums[mid]){
right = mid-1;
} else {
return mid
}
}
return -1;
};枚举
顺次数-1291
我们定义「顺次数」为:每一位上的数字都比前一位上的数字大 1 的整数。
请你返回由 [low, high] 范围内所有顺次数组成的 有序 列表(从小到大排序)。
示例 1:
输出:low = 100, high = 300
输出:[123,234]示例 2:
输出:low = 1000, high = 13000
输出:[1234,2345,3456,4567,5678,6789,12345]提示:
10 <= low <= high <= 10^9题解:
首先根据提示写出最大的顺序次数,那么其他的顺序次数就是这个数的截取部分了,我们可以直接两个循环进行枚举。
var sequentialDigits = function(low, high) {
const maxNum = '123456789';
let res = [];
for(let i = 0; i < maxNum.length-1; i++){
for(let j = i+1; j< maxNum.length;j++){
const num = Number(maxNum.slice(i,j+1));
if(num > high){
break;
} else if(num <= high && num >=low){
res.push(num);
}
}
}
return res.sort((a,b) => a-b);
}矩阵
螺旋矩阵-54
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:
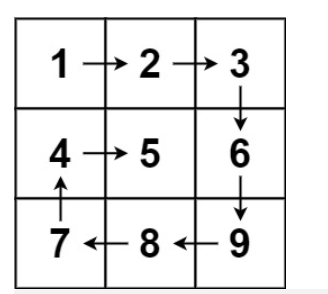
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]示例 2:
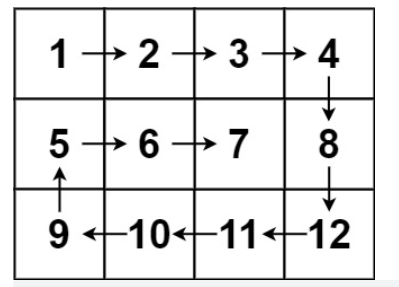
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]提示:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100题解:
记录一个 visited 数组,从 0, 0 开始,按照右 -> 下 -> 左 -> 上的方向不断前进,直到遇到边界或者已经访问过的元素 则切换成下一个方向,每访问一个元素就把结果放入 res 数组中,最终当 res 的长度和矩阵大小一致时,就返回结果。这里方向用 dirs 表示 4 个方向对应的偏移坐标,通过 currentIndex 指针不断递增来维护当前的方向,由于可能会超出方向数组的长度,所以每次取值都对 4 取余即可。
var spiralOrder = function(matrix) {
let curDirIndex = 0;
// 右-> 下-> 左 -> 上
const directions = [
[1,0],
[0,1],
[-1,0],
[0,-1],
];
const res =[];
const maxX = matrix[0].length;
const maxY = matrix.length;
function inArea(x,y){
return x>=0 && y>=0 && x<maxX&& y<maxY;
}
// 记录是否已经被访问
const visited = new Array(maxY);
for (let i =0; i < visited.length; i++) {
visited[i] = new Array(maxX);
}
function search(startX, startY){
res.push(matrix[startY][startX]);
if(res.length === maxX*maxY) return;
visited[startY][startX] = true;
let [x,y] = directions[curDirIndex%4];
let nextX = x+startX;
let nextY = y+startY;
if(!checkDirection(nextX, nextY)){
// 超出范围或者已经被访问过就切换方向
[x,y] = directions[++curDirIndex%4];
nextX = x+startX;
nextY = y+startY;
}
search(nextX, nextY);
}
function checkDirection(x,y){
return (inArea(x, y) && !visited[y][x]);
}
search(0,0);
return res;
};螺旋矩阵 II-59
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:
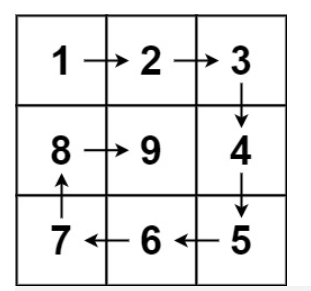
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]示例 2:
输入:n = 1
输出:[[1]]提示:
1 <= n <= 20题解:
该题和螺旋矩阵-54类似,代码拿来改改就行
/**
* @param {number} n
* @return {number[][]}
*/
var generateMatrix = function(n) {
// 按照右 -> 下 -> 左 -> 上的顺序进行生成
const directions = [
[1,0],
[0,1],
[-1,0],
[0,-1]
]
let curDirIndex = 0;
let num = 1;
// 生成二维数组
const maxX = maxY = n;
const matrix = new Array(maxY);
for(let y = 0; y< maxY; y++){
matrix[y] = new Array(maxX);
}
// 判断是否越界
const isValid = (x,y) =>{
return x>=0&&y>=0&&x<maxX&&y<maxY;
}
const isVisited = (x, y) => {
return matrix[y][x]
}
function checkPath(x,y){
return isValid(x,y) && !isVisited(x, y);
}
const helper = (startX, startY) => {
matrix[startY][startX] = num++;
if(num > n*n) return matrix;
let [x,y] = directions[curDirIndex%4];
let nextX = x+startX;
let nextY = y+startY;
if(!checkPath(nextX,nextY)){
// 改变方向
[x,y] = directions[++curDirIndex%4];
nextX = x+startX;
nextY = y+startY;
}
helper(nextX,nextY);
}
helper(0,0)
return matrix;
};矩阵置零-73
给定一个 *m* x *n* 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
示例 1:
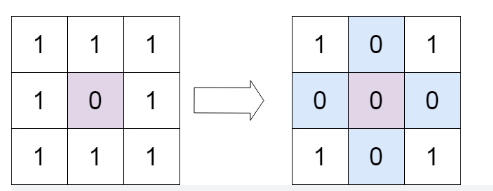
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]示例 2:
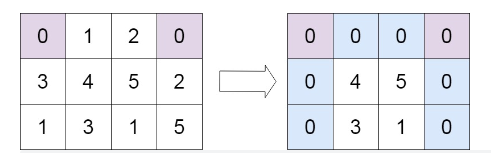
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]提示:
m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
-2^31 <= matrix[i][j] <= 2^31 - 1题解:
简单思路:
- 首先遍历矩阵,将数值为零的坐标保存起来
然后在遍历所有为0的坐标,处理该坐标的行列为0 ,同时缓存记录该坐标的行或列已经处理为0了,已经处理为0的行或者列就不需要进行处理了。
/** * @param {number[][]} matrix * @return {void} Do not return anything, modify matrix in-place instead. */ var setZeroes = function(matrix) { const maxY = matrix.length; if(!maxY) return; const maxX = matrix[0].length; const zeros = [] const zeroCol=[]; const zeroRow=[]; // 遍历记录所有的0点 for(let y=0; y<maxY; y++){ for(let x=0; x<maxX; x++){ if(matrix[y][x] === 0){ zeros.push([x,y]); } } } for(let zero of zeros){ const [x,y] = zero; if(!zeroCol[x]){ for(let i=0;i<maxY;i++){ matrix[i][x]=0; } zeroCol[x]=true; } if(!zeroRow[y]){ for(let j=0;j<maxX;j++){ matrix[y][j]=0; } zeroRow[y]=true; } } return matrix };
进阶思路:
空间复杂度为常数的做法:
- 利用两个flag记录第一行第一列是否有0
- 遍历除第一行第一列以外的矩阵元素,如果有元素为0,则将对应的第一行第一列的位置置为0
- 同样遍历除第一行第一列以外的矩阵元素,如果
matrix[i][j]所在位置的第一行第一列有任意一个位置为0 那么那个位置将被置为0 - 根据两个flag决定是否将第一行第一列置为0
/**
* @param {number[][]} matrix
* @return {void} Do not return anything, modify matrix in-place instead.
*/
var setZeroes = function(matrix) {
const maxY = matrix.length;
if(!maxY) return;
const maxX = matrix[0].length;
let rowFlag = false;
let colFlag = false;
for(let x=0;x < maxX;x++){
if(matrix[0][x] === 0){
rowFlag = true;
break;
}
}
for(let y=0;y < maxY;y++){
if(matrix[y][0] === 0){
colFlag = true;
break;
}
}
for(let y=1; y < maxY;y++){
for(let x=1; x < maxX;x++){
if(matrix[y][x] === 0){
matrix[y][0] = 0;
matrix[0][x] = 0
}
}
}
for(let y=1; y < maxY;y++){
for(let x=1; x < maxX;x++){
if(matrix[0][x] === 0|| matrix[y][0] ===0){
matrix[y][x]=0
}
}
}
if(rowFlag){
for(let x=0; x < maxX; x++){
matrix[0][x]=0;
}
}
if(colFlag){
for(let y=0; y < maxY; y++){
matrix[y][0]=0;
}
}
return matrix;
};
黄金矿工-1219
你要开发一座金矿,地质勘测学家已经探明了这座金矿中的资源分布,并用大小为 m * n 的网格 grid 进行了标注。每个单元格中的整数就表示这一单元格中的黄金数量;如果该单元格是空的,那么就是 0。
为了使收益最大化,矿工需要按以下规则来开采黄金:
每当矿工进入一个单元,就会收集该单元格中的所有黄金。
矿工每次可以从当前位置向上下左右四个方向走。
每个单元格只能被开采(进入)一次。
不得开采(进入)黄金数目为 0 的单元格。
矿工可以从网格中 任意一个 有黄金的单元格出发或者是停止。
示例 1:
输入:grid = [[0,6,0],[5,8,7],[0,9,0]]
输出:24
解释:
[[0,6,0],
[5,8,7],
[0,9,0]]
一种收集最多黄金的路线是:9 -> 8 -> 7。示例 2:
输入:grid = [[1,0,7],[2,0,6],[3,4,5],[0,3,0],[9,0,20]]
输出:28
解释:
[[1,0,7],
[2,0,6],
[3,4,5],
[0,3,0],
[9,0,20]]
一种收集最多黄金的路线是:1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7。提示:
1 <= grid.length, grid[i].length <= 15
0 <= grid[i][j] <= 100
最多 25 个单元格中有黄金。题解:此题也是可以利用递归与回溯的基本模板,首先定义好四个方向的坐标,遍历每个方向,当遇到边界或者为0的点位是就切换方向进行递归,直到所有可尝试的点位都已经访问到。
注意点,每次遍历下一个格子前的判断:
- 下一个格子没有超出边界
- 下一个格子的值大于0
- 没有被访问过,这里可以将访问过的格子赋值为0来进行记录,等到相应轮次的递归结束后再还原
var getMaximumGold = function(grid) {
const maxY = grid.length;
if(!maxY) return;
const maxX = grid[0].length;
let maxGold = 0;
const directions = [
[1,0],
[0,1],
[-1,0],
[0,-1]
];
// 边界问题
function isValid(x,y){
return x>=0 && y>=0 && x<maxX && y<maxY;
}
function helper(startX, startY, prevGrid){
let cur=prevGrid+grid[startY][startX];
maxGold = Math.max(maxGold, cur);
let pgrid = grid[startY][startX]
grid[startY][startX] = 0;
// 尝试每一个方向是否可继续递归
for (const direction of directions) {
let [x,y] = direction;
let nextX = startX+x;
let nextY = startY+y;
// 不满足条件就换方向
if(!isValid(nextX, nextY) || grid[nextY][nextX]===0){
continue;
} else {
helper(nextX, nextY,cur);
}
}
//还原
grid[startY][startX] = pgrid;
}
for(let y=0; y<maxY; y++){
for(let x=0; x<maxX; x++){
// 从第一个不为0的点开始
if(grid[y][x]===0) continue;
helper(x,y,0)
}
}
return maxGold;
};动态规划
最长的斐波那契子序列的长度-873
如果序列 X_1, X_2, ..., X_n 满足下列条件,就说它是 斐波那契式 的:
n >= 3
对于所有 i + 2 <= n,都有 X_i + X_{i+1} = X_{i+2}
给定一个严格递增的正整数数组形成序列 arr ,找到 arr 中最长的斐波那契式的子序列的长度。如果一个不存在,返回 0 。
(回想一下,子序列是从原序列 arr 中派生出来的,它从 arr 中删掉任意数量的元素(也可以不删),而不改变其余元素的顺序。例如, [3, 5, 8] 是 [3, 4, 5, 6, 7, 8] 的一个子序列)
示例 1:
输入: arr = [1,2,3,4,5,6,7,8]
输出: 5
解释: 最长的斐波那契式子序列为 [1,2,3,5,8] 。示例 2:
输入: arr = [1,3,7,11,12,14,18]
输出: 3
解释: 最长的斐波那契式子序列有 [1,11,12]、[3,11,14] 以及 [7,11,18] 。提示:
3 <= arr.length <= 1000
1 <= arr[i] < arr[i + 1] <= 10^9题解:
比较简单的思路如下,首先双for循环以此遍历每一项x1和后一项x2,我们只需要保留前两项,并计算出和sum,再再数组里寻找是否有等于sum的数组项,如果有就更新前两项,将x2赋值给x1,sum赋值给x2,在计算出新的sum,然后再去寻找是否有符合条件的数组将,只要找到了就将计数cur加1,注意计数是从2开始加的,最后再将计数最大的保留下来,返回即可。此题可以优化寻找sum的地方,可以使用map来进行优化,当然这里提议是提供一个严格递增的数组,使用二分查找也是比较合适的。
var lenLongestFibSubseq = function(arr) {
let max = 2;
for(let i = 0; i< arr.length-1; i++){
for(j=i+1; j< arr.length;j++) {
let x1 = arr[i];
let x2 = arr[j];
let sum = x1+x2;
let cur = 2;
// 向后找是否有一项等于sum
while(arr.binarySearch(sum)>=0){
x1 = x2;
x2 = sum;
sum = x1+x2;
cur++;
}
max = Math.max(max,cur);
}
}
return max < 3 ? 0: max;
};
Array.prototype.binarySearch = function(item) {
let left = 0;
let right = this.length-1;
while(left <= right) {
let mid = Math.floor((left+right)/2);
if(item < this[mid]){
right = mid-1;
} else if(item > this[mid]){
left = mid+1;
} else {
return 1;
}
}
return -1;
}最长重复子数组-718
给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。
示例 1:
输入:nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出:3
解释:长度最长的公共子数组是 [3,2,1] 。示例 2:
输入:nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
输出:5提示:
1 <= nums1.length, nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 100题解:
/**
*
* @param {*} nums1
* @param {*} nums2
* @returns
* 推导动态方程
* 首先dp[0][0] = 0;
* 当i ,j 大于等于1的时候
* dp[i][j] = dp[i-1][j-1];
*
* 根据dp[i][j]的定义,dp[i][0] 和dp[0][j]其实都是没有意义的!
*
* 但dp[i][0] 和dp[0][j]要初始值,因为 为了方便递归公式dp[i][j] = dp[i - 1][j - 1] + 1;
所以dp[i][0] 和dp[0][j]初始化为0。
举个例子A[0]如果和B[0]相同的话,dp[1][1] = dp[0][0] + 1,只有dp[0][0]初始为0,正好符合递推公式逐步累加起来。
*/
var findLength = function(nums1, nums2) {
let max = 0;
const dp = new Array(nums1.length+1).fill(0).map(item => new Array(nums2.length+1).fill(0))
for(let i = 1; i <= nums1.length; i++) {
for(let j = 1; j <= nums2.length; j++) {
if(nums1[i-1] === nums2[j-1]) {
dp[i][j] = dp[i-1][j-1] + 1;
}
max = Math.max(dp[i][j], max);
}
}
console.log(dp);
return max;
};

Comment here is closed