红黑树
基本规则
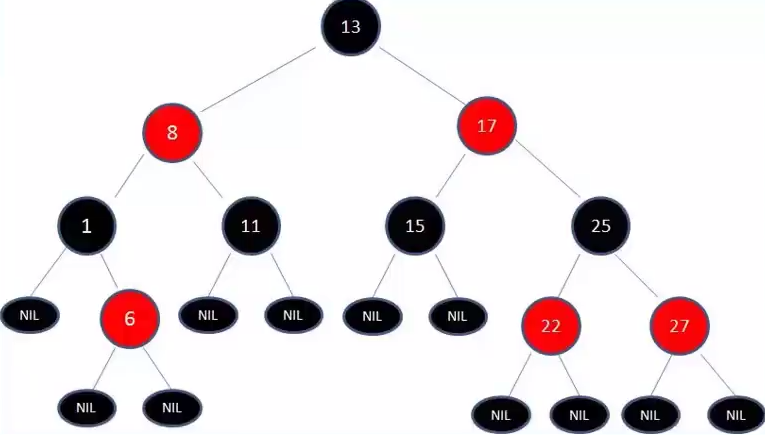
首先满足二叉搜索树的基本规则,另外还有以下一些特性:
- 节点是红色或者黑色
- 根节点是黑色
- 每个叶子节点都是黑色的空节点(NIL节点)
- 每个红色节点的两个子节点都是黑色(从每个叶子节点到根的所有路径上不能有两个连续的红色节点)
- 从任意节点到其每个叶子节点的所有路径都包含相同数目的黑色节点
红黑树插入操作
插入新节点要保证仍然符合红黑树的规则,这里有三种操作方式来保证:
变色--左旋转--右旋转
设要插入的节点为N,其父节点为P,其祖父节点为G,其叔叔(祖父的另外一个子节点)节点为U
情况一
新节点N位于树的根上(第一个节点),没有父节点,直接将颜色变为黑色即可(我们默认插入的都为红色的节点)
情况二
新节点的父节点P是黑色,直接插入,新节点左右子节点设置为黑色NIL,其余无需变化
情况三
P为红色,U为红色, 父节点P和叔节U点变为黑色,祖父节点G变为红色,若祖父节点G就为根节点那么祖父节点G再变为黑色,反之就将祖父节点G视为新插入节点,考虑是否满足其他情况再进行变换
情况四
N的父亲节点P为红色,叔叔节点U为黑色节点,祖先节点G为黑色,且N为左节点,父亲节点P改为黑色,祖父节点G改为红色,然后对祖父节点G进行右旋转
情况五
N的叔叔节点为黑色节点,且N为右节点,以P为根进行左旋转 ,将P节点作为新插入的红色节点考虑,自己N变为黑色,祖父G变为红色,以祖父节点G为根进行右旋转
案例练习
依次插入10,9,8,7,6,5,4,3,2,1
插入10:由于新节点10就位于树的跟上,满足情况一,所以直接插入,将颜色改为黑色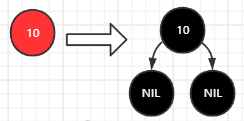
插入9:新节点9的父节点10为黑色,满足情况二,直接插入,其余无变化(之后图片都省略了NIL节点)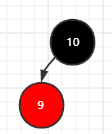
插入8:新节点8的父节点9为红色,叔叔节点NIL为黑色,祖先节点10为黑色,而且新节点8为左节点,满足情况四,需要以祖父节点10为根右旋转,再将祖父节点10改为红色,父亲节点9改为黑色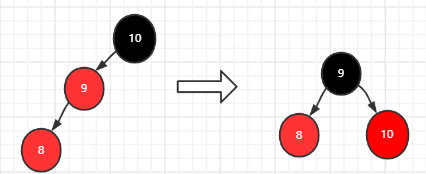
插入7:新节点的父亲节点8和叔叔节点10都为红色,满足情况三,就向上依次变色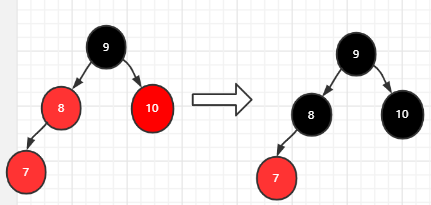
插入6:新节点6的父节点7为红色,其叔叔节点NIL为黑色,祖父节点8为黑色,而且新节点6为左节点,满足情况四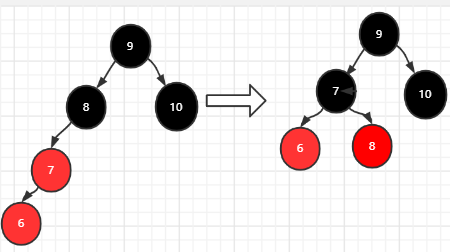
插入5:新节点的父亲节点和叔叔节点都为红色,满足情况三,只需变色即可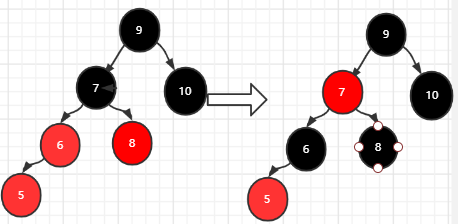
插入4:同理满足情况四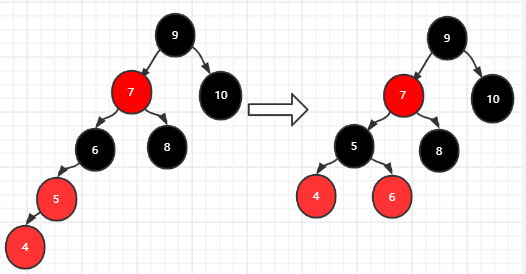
此时的红黑树依然满足最长路径不超过最短路径的两倍
插入3:首先满足情况三,变换后遇到了祖父节点5的父节点7也为红色,这里我们需要将祖父节点5看成新插入的节点,那么此时的祖父节点5的父节点7为红色,叔叔节点10为黑色,祖先节点9为黑色,所以又满足了情况四,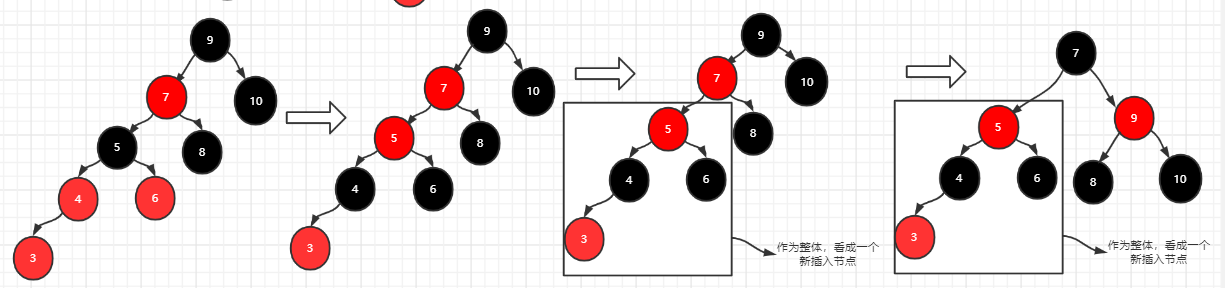
插入2:满足情况四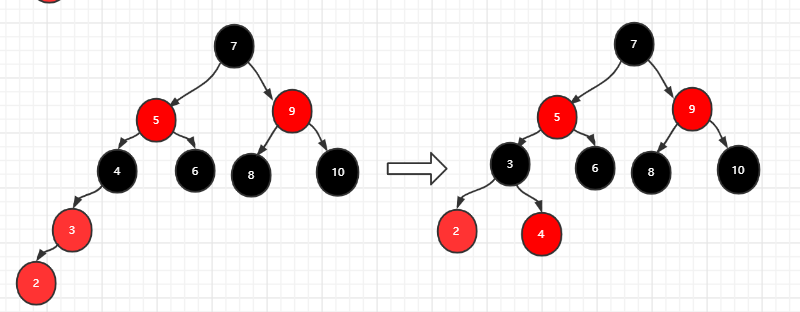
插入1:满足情况三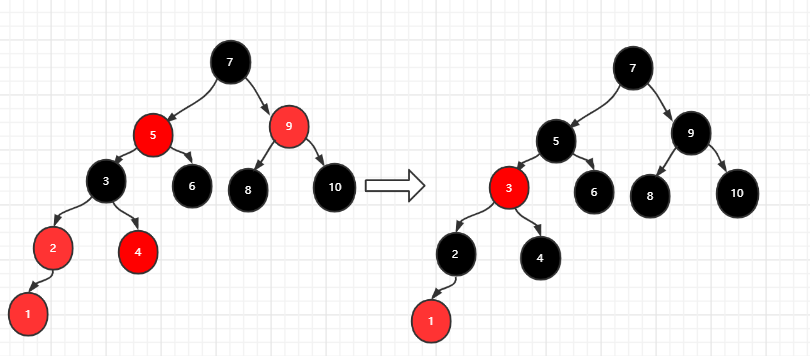
TODO:实现插入代码
TODO:实现删除代码

Comment here is closed