斐波那契的几种实现方式

斐波那契数组为 0 1 1 2 3 5 8....

1.普通递归方式

function fib(n) {
  if(n <= 1) return n;
  return fib(n - 2) + fib(n - 1);
}

//测试耗时（仅供参考）
testTime(() => {
  console.log(fib(30));
})
function testTime(cb) {
  let begin = Date.now();
  cb();
  let after = Date.now();
  console.log("消耗时间: "+ (after - begin) +" ms");
}

输出结果：

832040
消耗时间: 15 ms

2. 递归优化版

普通的递归方式在遇到n稍大的时候，会很久不出结果，比如n=64的时候基本算不出来

对于普通的递归我们分析其时间复杂度就可以发现，其中出现了很多的重复计算，比如计算n=6，步骤如下图：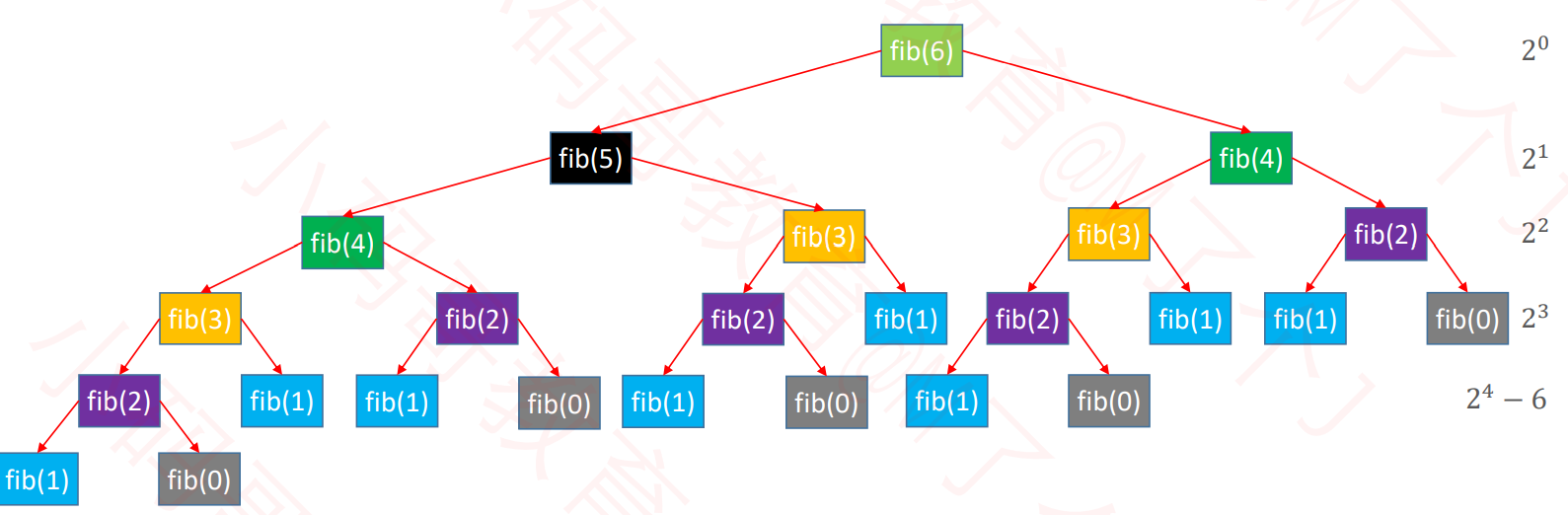

计算fib6的时候需要计算fib5和fib4，而fib5需要fib4和fib3，这里fib4就重复计算了，而且我们可以通过上述的步骤发现该算法的时间复杂度约为2^n， 效率极其不佳。

优化思路，利用一个数组记录我们算过的fib结果，当需要使用的时候直接用，就不需要在重新计算了

let array = []; 
function fib1(n) {
  if(n <= 1) return n;
  if(array[n] !== undefined) {
    return array[n];
  }
  array[n] = fib1(n - 2) + fib1(n - 1);
  return array[n];
}

运算结果：

832040
消耗时间: 4 ms

3. 非递归方式

function fib3(n){
  if(n <= 1) return n;
  let fir = 0;
  let sec = 1;
  for(let i = 0; i < n - 1; i++) {
    sec += fir;
    fir = sec - fir;
  }
  return sec;
}

运算结果：

832040
消耗时间: 5 ms

这里的时间复杂度就为O（n）了

4. 通项公式

斐波拉契通项公式如下：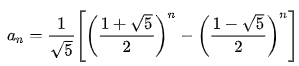

代码如下：

function fib4(n){
  let c = Math.sqrt(5);
  return parseInt((Math.pow((1 + c) / 2, n) - Math.pow((1 - c) / 2, n)) / c);
}

运算结果：

832040
消耗时间: 4 ms

总结

我们的算法优化基本是用尽量少的存储空间和尽量少的执行时间，需要根据数据量来选择最合适的算法，没有绝对的算法，我们根据情况可以时间换空间，空间换时间。
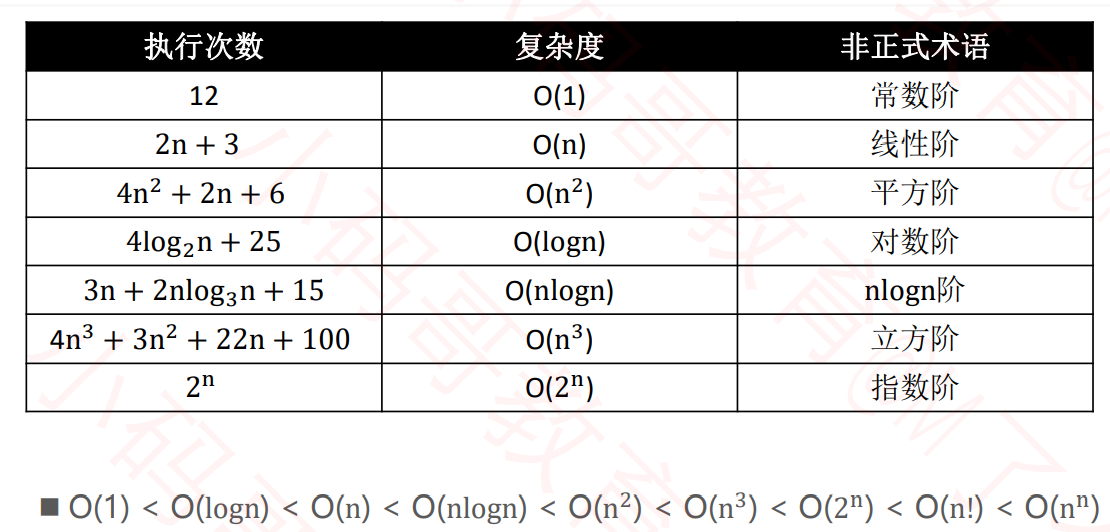
常见的复杂度：